本文是以文末参考文献[2]为主要参考的读书笔记，建议读者阅读参考文献[2],比本文高明多了。

由于wordpress的markdown转换不是很好看，可查看本文的另一个html版本。

基本名词

词条（Lemma）或引用形式（citation form）

指的是一个词典或者词库中的一个单词条目。表示了一个词的基本形式和大致的含义。譬如对于 sing、sung、sang，它们的 Lemma 都是 sing，carpets 的 Lemma 是 carpet。

 

词形（Word Form）

词形：一个词在使用时的灵活用法。

Wordform	Lemma
banks	bank
sung	sing
duermes	dormir

词义（Word Sense）

即使有了 Lemma 和 Wordform，一个 Lemma 还是有可能有多种含义，譬如对于 bank 这个单词，具有银行和堤岸这两种含义，我们就把这每一种含义都称作一个 Word Sense (词义)。

同名（Homonymy）

我们把 Lemma 的这种具有多个不同的、不相关的含义的现象叫做同名（Homonymy ）。 这其中包括两种： – 同形（Homographs）：两个 Lemma 字面长的一样。譬如 bank（银行） 和 bank （河岸） – 同音（Homophones）：两个 Lemma 读音一样。譬如Write 和 right，Piece 和 peace

正是同名的存在，导致了自然语言处理中很多棘手的问题。

一词多义（Polysemy）

当一个词具有多种含义时，如果两种含义具有相关性，我们就不把它们称为同名（Homonymy），而是称为一词多义（polysemy）。

仍然以 bank 这个单词为例，bank（1）的含义是金融机构银行，bank（2）的含义是海岸，bank（3）的含义是生物存储库，譬如blood bank（血库）, egg bank（卵子库）, sperm bank（精子库）。可以看出 bank（3）和 bank（2）有一些联系，银行和生物存储库都是存储一些物品的，只不过银行存的是钱相关的东西，生物存储库指的是存储了一些生物上的物品。

词义消岐（Word sense disambiguation）

词义消岐就是要确定特定上下文中的一个单词，究竟用的是哪一个词义（Word Sense）。词义消岐在计算语言学和诸如机器翻译、自动问答等任务中已经有很长的研究和应用历史。

同义（Synonyms）

当两个单词的两个语义（Sense）相同或者几乎相同时，我们称这两个语义是同义的。

词的相似度

如何度量词与词之间的相似度?
分布假设 （John Firth, 1957） A word is characterized by the company it keeps 一个单词可以用和它共生的单词来刻画。

譬如,对于单词 tesgüino,考察以下语句 A bottle of Tesgüino is on the table.
Everybody likes tesgüino.
Tesgüino makes you drunk.
We make tesgüino out of corn 可以总结出 tesgüino 的共生词以及句法特征： – 可以出现在 drunk 之前 – 可以出现在 bottle 之后 – 可以直接接在 likes 后面

考虑如上共生关系，我们就可以认为，Tesgüino 和bear，wine，whiskey 是类似的词，可以猜测 Tesgüino 是一种发酵酒精饮料，用玉米发酵而成。

上面提出了度量单词相似度的基本出发点，那么我们具体怎么计算相似度呢？

对于给定的具有 n 个单词的词汇表，我们可以把其中的单词 w 表示成这种形式：
w = (f1,f2,f3,...,fn) 其中fn表示：词汇表中的第n个词在 w 的上下文(即)中是否出现（一个二值类型）或者出现的次数。因此 tesgüino 可以表示为： tesgüino = (1,1,0,...) 第一个1表示和 corn 一起出现，第二个1表示和 drunk 一起出现，第三个 0 表示和matrix 这个单词不在一起出现。可能性

基于如上单词的表示方法，我们就可以进行距离指标来度量单词之间的相似度。譬如使用常见的余弦距离,可以算出一个-1到1之间的值来表示两个词的相似度。-1表示完全不相关，1表示完全相同。

向量空间模型

向量空间模型是一种词义的表示方式。其基本出发点是将词嵌入到一个向量空间中，正因此，我们把一个词的向量表示称为一个词嵌入（embedding），又翻译词向量（下文两个叫法混用）。与之相反的，在很多传统的 NLP 应用中，一个单词由单词在词汇表中的索引来表示，或者用字母组成的字符串来表示。向量模型的一大优势在于，他可以更加细粒度的表示一个词的语义，而非像一个索引，一个字符串那样把单词看作一个原子。

向量空间模型已经在 NLP 领域使用超过50年了。被广泛应用于命名实体抽取、语义角色标注和关系抽取等过程。此外，向量模型也是计算词相似度、句相似度、文本相似度的最普遍的方式，在一些实践应用如自动问答、摘要、自动文章评分上也有应用。

向量和文档

词-文档矩阵（term-document matrix）

词-文档矩阵的行表示的是词汇表中的单词，列是文档。矩阵中的元素表示的是一个词在一个文档中出现的次数。 譬如下表就是一个词-文档矩阵。行是莎士比亚的几部戏剧，列是我们选择的4个词，表中每个元素表示了该词的在戏剧中的出现次数。

–	As You Like It	Twelfth Night	Julius Caesar	Henry V
battle	1	1	8	15
soldier	2	2	12	36
fool	37	58	1	5
clown	5	117	0	0

词-文档矩阵可以用来做什么？
词-文档矩阵中的每个列可以用来表示一个文档。我们可以把一个文档看作是|V|维-空间的一个点,这个点的维度是词汇表的词汇量，每个维的值是词汇的出现频数。

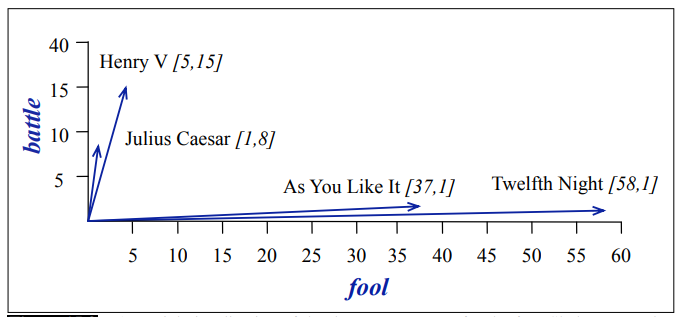
如上图，我们用二维来刻画莎士比亚的四篇戏剧。可以直观的发现，Henry V （《亨利五世》）和 Julius Caesar（《凯撒大帝》） 更加偏向于 battle （战斗），而 As You Like It （《皆大歡喜》）和 Twelfth Night（《第十二夜》）更加偏向于 fool 这个词，这似乎可以用后两者是戏剧来解释。

词-文档矩阵最初发明于信息检索（information retrieval）领域，直觉出发点是：两个相似的文档趋向于有相似的词汇,而两个文档如果有相似的词汇，那么它们的词-文档矩阵也趋向于是相似的。至于如何量化这个相似，我们将在下文介绍,包括tf-idf权重、余弦距离。

用向量来表示词

上文中我们用向量表示了文档，类似的，词也可以用向量来表示。在term-document matrix中，对于词来说，词向量不是一个列向量，而是一个行向量，每一行可以用来刻画一个词。文档向量的特性在词向量上也可以使用：对于文档来说，相似的文档有相似的文档向量，那么对于词来说，相似的词也具有相似的词向量。

值得注意的是，词向量一般不使用文档来刻画词，而是使用上下文（contex）来刻画词，也就是说列列不再是文档名，而是上下文中的词，这样可以更加细粒度的刻画一个词。因此，我们的矩阵将是一个|V|*|V|维的矩阵。行和列都是训练集中的词汇，矩阵元素表示两个词汇出现在同一个上下文中的次数。这里的同一个上下文可以是“同一个文档”，那么矩阵元素值就是两个单词出现在同一个文档中的次数，更普遍的，我们一般采用一个更小的滑动窗口来定义两个单词出现在同一个上下文中，譬如出现在左右4个单词的范围内，也就是说列单词出现在行单词左边或右边4个单词范围内的次数。

下表展示了来自Brown数据集的其中四个单词的共生矩阵（采用7-词上下文窗口，7-word windows surrounding），

–	aardvark	…	computer	data	pinch	result	sugar	…
apricot	0	…	0	0	1	0	1
pineapple	0	…	0	0	1	0	1
digital	0	…	2	1	0	1	0
information	0	…	1	6	0	4	0

可以看出，apricot 和 pineapple 是相似的，因为它们的上下文中都出现了 pinch 和 sugar，但是 digital 的上下文就没有这些词。因此可以发现，词的关系似乎潜藏在这个矩阵之中。

既然已经有了基本直觉出发点，接下来我们来考察如何定量计算词与词之间的关系。

点互信息（Pointwise Mutual Information ，PMI）

为什么需要定量计算词与词之间的关系？
上文中的四个单词的共生矩阵中，我们已经可以看出词与词之间的关系了，但是由于是原始数量统计，需要考察很多数字，如果直接用一个指标来定量表示词与词之间的关系，就会方便很多。

此外，还存在另一个问题：the，it这些词非常常见，在共生矩阵中，看起来几乎所有词都和他们相关度很高，我们需要区分 apricot 和 pineapple 的相似关系比 pineapple 和 the 的相似关系更强。

对此，Church 和 Hanks（1989，1990)基于互信息提出了点互信息（Pointwise Mutual Information ，PMI）的概念。

互信息（MI）与点互信息（PMI）

互信息是信息论中的概念。用来衡量两个随机变量之间的相关性。其公式是：

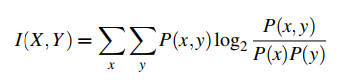
MI 表示的是在了解了其中的一个 Y 的前提下，对消除另一个 X 不确定性所提供的信息量。

Fano（1961）提出，对于两个点（单词）, x 和 y，有概率 P(x) 和 P(y),那么他们的互信息，定义为：

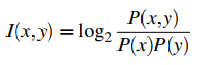
这个公式，通俗的说起来就是，我们对比：将 x 和 y 绑定时的观察到的概率 和 对 x 和 y 单独观察得到的概率。如果 x 和 y 的相关度很高，P(x,y)将会远大于P(x)P(y)，此时 I(x,y)>>0；如果 x 和 y 没啥关联，那么P(x,y)≈P(x)P(y),此时 I(x,y)≈0；如果 x 和 y 在互补分布（在语言学中，当两个语言成分不能在同一个环境中出现，称为互补分布）中，那么 P(x,y)将会远小于P(x)P(y)，此时 I(x,y)<<0。

我们把这个想法应用于词的共生矩阵中，就可以定义目标词 w 和 上下文词 c 之间点互信息（Pointwise Mutual Information ，PMI）：

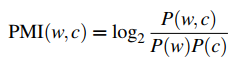
PPMI

点互信息的取值范围从负无穷到正无穷。本来，PMI 为负表明两个单词在一起出现的概率比随机的还小，说明两个词有互斥关系，很少一起出现，但在实际数据集计算中，负值我们几乎观察不到，除非我们的数据集足够大：

考虑单词 x 和 单词 y 的出现概率，假设都是 10e-6，即 P(x)=P(y)=10e-6，假如 x 和 y 基本上没什么关系，那么P(x,y)=P(x)P(y)=10e-12，此时 PMI(x,y)=0。如果我们看到了 PMI(x,y)<0 的情况，那么我们就有 P(x,y)<10e-12，所以说想观察到PMI小于零出现的概率会变得很小。概率太小，如果数据集不足够大，我们就没有足够的置信度来支持 x 和 y 的互斥关系。

因此，我们一般用 PPMI （Positive PMI），干脆直接把 PMI 中的负值替换成0（Church and Hanks 1989, Dagan et al. 1993, Niwa and Nitta 1994)

这不仅解决了负值不可靠的问题，还解决了log(0)无法计算的问题。

词与词的度量指标定义好了！现在我们可以对词的共生矩阵进行运算了！

假设我们的共线矩阵 F 具有 W 行 和 C 列，fij 表示单词 wi 出现在上下文词ci周边的次数，那么我就可以把这个共线矩阵转化成一个 PPMI 矩阵，该矩阵的 PPMIij 表示单词 wi 和上下文词 ci 之间的 PPMI 值：

应用上述公式对前文提到的四个单词的共生矩阵计算联合概率分布矩阵如下：

–	computer	data	pinch	result	sugar	p(w)
apricot	0	0	0.05	0	0.05	0.11
pineapple	0	0	0.05	0	0.05	0.11
digital	0.11	0.05	0	0.05	0	0.21
information	0.05	.32	0	0.21	0	0.58
p(context)	0.16	0.37	0.11	0.26	0.11

再基于此，计算 PPMI 矩阵：

–	computer	data	pinch	result	sugar
apricot	0	0	2.25	0	2.25
pineapple	0	0	2.25	0	2.25
digital	1.66	0	0	0	0
information	0	0.57	0	0.47	0

PMI 的缺陷与修正

PMI 偏向于很少发生的事件，一些很罕见的单词往往拥有较高的 PMI。

一种解决方案是，对 P(c) 的计算方法稍加改变，换一个计算Pα(c)的函数:

Levy et al. (2015) 发现 α = 0.75 的时候，效果较好。其原因是，当上下文词 c 很罕见时，本来 P(c) 会很小，从而 PPMI 很高，α = 0.75，降低了 Pα(c) 的值，从而降低了 PPMI 的值。

另一种解决方案是采用拉普拉斯平滑。给共生矩阵中所有值增加一个很小的增量（一般0.1-3之间）。对上文数据集做add-2拉普拉斯平滑后，PPMI 矩阵如下：

–	computer	data	pinch	result	sugar
apricot	0	0	0.56	0	0.56
pineapple	0	0	0.56	0	0.56
digital	0.62	0	0	0	0
information	0	0.58	0	0.37	0

可以观察一下不做任何处理的 PPMI 矩阵和我们使用拉普拉斯平滑后的 PPMI 矩阵，以PPMI(information,data) 和 PPMI(pineapple,sugar)为例对比就可以发现，本来由于pineapple和sugar比较罕见，他们的 PPMI 值很高，而 information 和 data 之间的关联其实和(pineapple,sugar)差不多，但由于这两个词很常见，导致 PPMI 值远低于前者。平滑后效果好了一些。

替代 PPMI 衡量关联度的指标

上文介绍了 PMI 可以衡量词与词（或者其他特性）之间的关联。然而 PPMI 并不是唯一可用的指标。来自信息论（tf-idf, Dice）以及假设检验（t-test, the likelihood-ratio test）也可以测度关联度。
Tf-idf
Tf-idf由两部分组成。

• term frequency (Luhn, 1957)，词频。直接计数词在文档中的出现频数，当然有可能对其取个对数log。
• inverse document frequency(Sparck Jones, 1972)，或者IDF term weight，逆文本频率指数。IDF是为了给那些只出现在少量文档中的词赋予更高的权重。IDF由分式 N/dfi 定义，其中 N 是文档个数。dfi 指的是词在多少个文档中出现。因此出现在越少的文档中的词权重越高。如果一个词在所有文档中都出现，那么权重就等于1。由于一般数据集很大，文档数量很大，我们一般对结果取对数：IDFi = log(N/DFi)。

将tf和idf组合起来就形成了一个特定组合tf-idf，公式如下，是用来评价第 i 个单词在第 j 个文档中的值。

wij = tfij * idfi

t-test
就是用假设检验的手段来推翻两个词不具有关联度的假设。具体细节，暂时跳过。

t-test(a,b) = P(a,b)−P(a)P(b)/√P(a)P(b)

衡量相似度：余弦距离

余弦距离是迄今为止测量两个向量相似度的最常用的指标。首先我们对相似的直觉出发点是：如果两个向量各个维度取值越相近，那么我们认为两个向量越相似。

为了定量测量相似，我们先考虑向量点积运算：

点积运算的结果和相似度是有一定关系的。两个向量如果同一个维度上都取值较大，那么点积就越大，反之，如果两个向量在不同的维度上取0，也就是各维度垂直的向量，那么点积=0，我们可以认为他们相似性很弱。

因此，粗略的来说，向量点积就可以作为相似性度量。其取值范围是负无穷到正无穷。

点积的几何意义

a·b = |a|·|b|·cosθ

问题与修正

使用点积作为相似性度量有个问题，向量长度越长时，点积一般越大：因为对于共生矩阵的行来说，context 越多，一般会有越多的词共生，而点积是由各维度乘积求和，所以点积越大。我们希望对不同的共生矩阵中的向量比较相似度。对此我们可以对结果正则化。

一个基本思路就是把点积除以两个向量的长度的积，这恰好和两个向量的余弦值是一致的，因此我们把它称为余弦相似度：

cosθ = (a·b) /(|a|·|b|)

其他相似度度量指标：

Jaccard 系数

假设两个向量的各维度总一个取值是0，那么sim=0。如果两个向量完全一样，则sim=1。分母是用来归一化的。
Dice

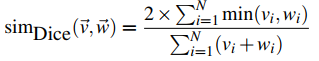
和 Jaccard 相似度量差不多。

除此之外，从信息论的分布相似性度量发展出了一系列相似性度量方法。它们的基本出发点都是：假设有两个向量v，w，我们把他们的维度值归一化使和为1，于是每一个向量就表示一个概率分布，我们可以认为，两个词相似，其表示的向量的概率分布也相似。因此问题转化为如何评估两个概率分布相似。

最常见的评价两个概率分布相似的方法就是库伦贝尔散度（Kullback-Leibler divergence），又称KL 散度或者相对熵 （relative entropy）：

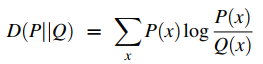
但是 KL 散度在Q(x) = 0 且 P(x) ≠ 0的时候没法计算。这就很致命，因为词分布矩阵是很稀疏的，很多词和上下文在数据集中是没有共生过的。基于此，Lee, 1999提出了JS 散度（Jensen-Shannon divergence）：

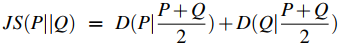
将两个分布加起来求平均从而避免了分母为0的尴尬。对于两个词的分布向量，我们可以改写如下：

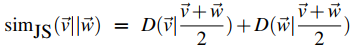
总结一下，所以现在对于计算关联度和相似度我们有以下指标了：

密集矩阵的语义学

前文我们已经提出了用稀疏向量表示词的方法，就是把一个词用和他共生词的共生数量作为向量的维度，这样产生的向量是一个稀疏向量。很多值等于0.维度太高显然并不利于机器学习算法和任务。本节我们考察如何将维度降低，将稀疏向量变成稠密向量。

主要包含三种方法： – 奇异值分解（SVD） – 神经网络的方法:skip-gram 或 CBOW – 一种基于临近词的方法：布朗聚类（Brown clustering）

奇异值分解（SVD，singular value decomposition）

奇异值分解（SVD）是一种生成稠密矩阵的经典方法，最初由Deerwester et al. (1988) 在潜在语义分析（LSA，Latent Semantic Analysis）中使用，用来从词-文档矩阵（term-document）生成词嵌入（embeddings）。

奇异值分解是一种找到数据集中最重要维度的方法，越重要的维度值的差别越大，该方法可以用于任意矩阵。 SVD 是用低维来近似高维数据集的方法之一，包括主成分分析（PCA）、因素分析（Factor Analysis）。

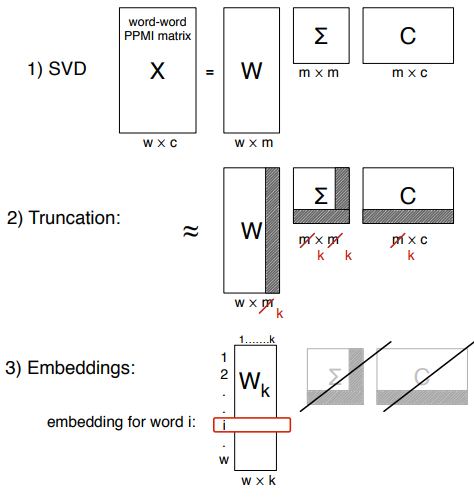
奇异值分解将一个矩阵分A解成三个矩阵的乘积：A=UDV(T)，其中 U 和 V 的列单位正交，D 为对角阵且对角元为正。对于任意矩阵 A，A的奇异值分解可以给出 A 的 k 阶最佳逼近。
我们省略细节。对于一个词-上下文共生 PPMI 矩阵（或者称词-词矩阵），通过 SVD 来获得词嵌入的过程如图所示。

通过预测过程获得词嵌入：Skip-gram 和 CBOW

通过预测过程获得词嵌入来源于神经网络语言模型：我们给定一个单词，来预测该单词的上下文。这个想法合理的主要直觉是：相似的词总是比较靠近。神经网络模型因此初始化一个随机的词向量，然后迭代如下过程：挨个考察语料的单词，调整词向量，让当前词和上下文词的相似度较高，让非上下文的单词和当前词的相似度较低。最终我们就可以得到词向量。

通过神经网络语言模型预测过程来获得词向量最流行的软件工具就是word2vec。该工具提供了获得词向量的两种方法：Skip-gram 和 CBOW （Mikolov et al. 2013, Mikolov et al. 2013a）

Skip-gram

其实和 SVD 类似，skip-gram 的训练事实上也是学习了两个矩阵，一个词嵌入矩阵 W 和一个上下文嵌入矩阵 C。W 和 C 分别是什么作用？我们先介绍一下 Skip-gram 的训练过程：

Skip-gram 的训练过程要解决的是一个预测任务：给定单词 w，预测 w 的上下文 c。为了完成这个预测任务，我们使用一个文本集（corpus）作为样本，假设文本集长度为 T，我们逐个单词考察 T 中的单词w(t)，（假设 w(t) 在词汇表中索引为 j，记为 wj）然后预测一个上下文窗口为 2L 的上下文词，譬如 L = 2时，我们对于 w(t)，预测[w(t-2), w(t-1), w(t+1), w(t+2)]。那如何预测这四个词呢？我们以 w(t+1)为例，也就是说如何预测一个词后面的一个词，假设后面的一个词在词汇表中的索引为k，也就是说我们希望计算出 P(wj|wk)最大的那个词，认为它就是我们预测出来的词。

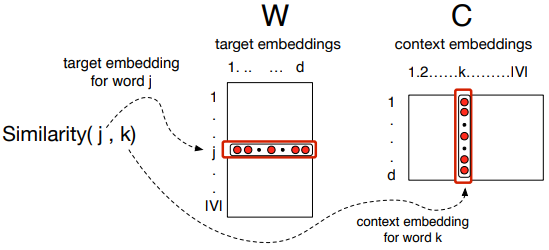
如何找到 P(wj|wk) 最大的那个 wk 或者说词汇表中的索引 k 呢？应用我们的直觉出发点：相似的词一般总是出现在一起，也就说相似的词出现在一起的概率更大。因此我们可以把最大化概率 P(wj|wk) 的问题，转变为最大化 wj 和 wk 的相似度问题。而相似度问题我们前文已经解决，可以用向量点积的值的大小来衡量相似度。对于当前单词 wj 和上下文词 wk，他们对应的向量记为 vj 和 ck，那么我们就可以计算向量内积 vj·ck 作为相似度。由于点积的范围时负无穷到正无穷，而我们现在希望用相似度来表示概率，因此可以使用softmax函数将其归一化，至此，可以定义：

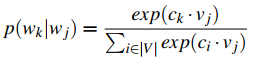
应用以上公式我们就可以进行预测任务的训练了。

CBOW (Continuous bag of words)

CBOW 是 skip-gram 模型的一个镜像。skip-gram 通过当前词预测前后上下文窗口的词，而 CBOW 通过前后上下文窗口的词预测当前词。其余并没有什么区别。

一般来说，CBOW 和 skip-gram 产生的结果会有轻微区别，且对于特定任务，一般其中一个更好。

负采样（Negative sampling）

上面（Skip-gram 小节）提到的计算概率的公式，对于分母的计算开销很大，我们需要计算词汇表中的每一个词w(t)与当前词的点积。分母其实是对词汇表中每个词进行了相似度统计，为了减少开销，我们可以使用负采样做一个分母的近似。

本来，分母中的词其实就分为两类，我们称为正样本和负样本，正样本就是文字集中当前单词周围的词；负样本（噪声样本）就是不在当前样本上下文的词。为了减少计算开销，我们可以只考虑正样本和负样本中与当前词最不相似的 k 个词：词汇表中加权一元概率较小的一些词。这就是负采样的基本过程。

采用了负采样后，对于当前词 w 和上下文词 c，我们的目标函数就是：

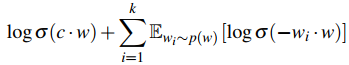
其中我们一般用

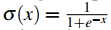
该目标函数表明，我们的目标是希望当前词和临近词共现的概率最大，和负采样的非临近词共现的概率最小。

至此，我们的神经网络模型中的预测目标就已经很清楚了，整个网络结构如下：

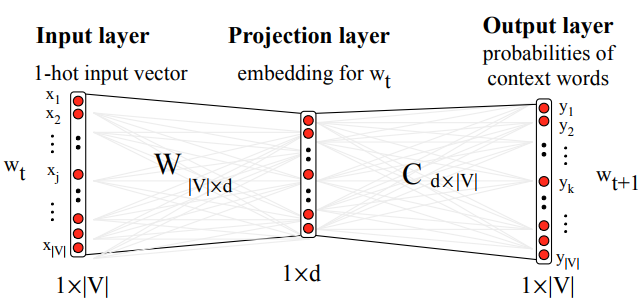
其中输入是单词的 1-hot 编码（只有一个维度为 1 的向量，向量维度总数等于词汇表大小），用于从词向量 W 中取出当前词对应的向量，其中 C 是上下文词向量。W 和 C 都是随机初始化的，通过训练过程不断调整。最终我们希望获得的产物就是 词向量矩阵 W。共 |V| 行，每一行对应词汇表中的一个词的词向量。

参考文献

[1]Kenneth Ward Church and Patrick Hanks. 1990. Word association norms, mutual information, and lexicography. Comput. Linguist. 16, 1 (March 1990), 22-29.
[2]Speech and Language Processing (3rd ed. draft).Chapter15.Vector Semantics
[3]cornell university.Spring 2017 CS5740: Natural Language Processing