wordpress的markdown生成的格式不是很好看，本文另外一个html版 。

本文就是个读书笔记，建议读者阅读文末参考文献2和3，比本文不知高到哪儿去了。

自然语言处理的概念

• 认知角度：理解语句
• 实践角度：生成语句

自然语言处理的两大途径

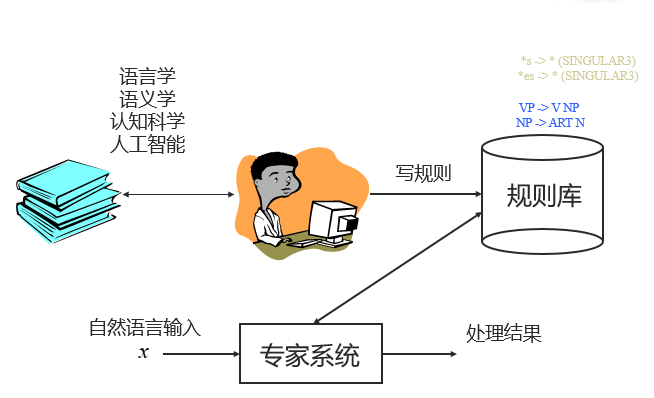
规则方法

被称为理性主义方法，主要依赖于人的总结。基于人工整理的 CFG （上下文无关文法，Context-Free Grammar） 规则，给出解决方案。

统计方法

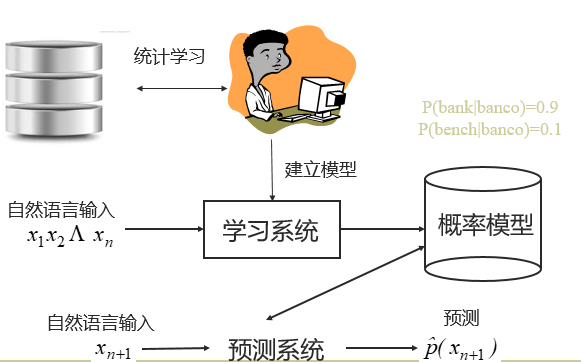
被称为经验主义方法，主要依赖于对数据的总结。从数据入手，利用统计机器学习方法解决问题。例如：通过自动学习得到PCFG（概率上下文无关文法），通过概率模型预测句法分析结果。

统计自然语言处理（Statistical NLP）

我们主要采用统计方法来进行机器学习。因此 统计自然语言处理的基本套路： – 问题形式化：将歧义问题转换成分类预测问题 – 语言的表示，建模：譬如n元模型 – 参数训练方法 – 有效的解码、推断

自然语言处理的基本框架

• 词层面
  • 语言模型
  • 分词
  • 词性标注（POS）
• 语法层面
  • 句法解析
• 语义层面
  • 命名实体识别（NER）
  • 语义角色标注（SR）
• 应用层面
  • 文本分类
  • 机器翻译
  • 自动问答
  • 情感分析

n元模型

统计语言模型

统计语言模型（Statistical Language Model）是一种History-based Model。 P(W)=P(w1w2…wn)=P(w1)P(w2|w1)
P(w3|w1w2)…P(wn|w1w2…wn-1) 定义：统计语言模型是用来刻画一个句子（词串序列）存在可能性的概率模型

该模型认为，语句中当前词是可以通过之前的词预测的。当然这个假设其实有些不切实际的，因为不可能总是通过过去的词预测将来的词。

统计语言模型为什么有用？

通过N元模型我们可以评估一个句子是人类写出来的句子的概率。也可以预测下一个词。那么这又有什么用呢？

有噪输入

首先概率是一个重要的基本信息，在一些有噪声的，或者模糊的输入中。譬如语音识别和手写输入。譬如电影《Take the money and run》中劫匪将纸条上"I have a gun"认错了，读成了“I have a gub”,如果我们应用n元模型计算句子的概率。就很容易知道"I have a gun"这个句子的可能性比“I have a gub”高，从而可以提出纠正。

机器翻译

计算句子的概率还可以应用于机器翻译。譬如一个粗劣的的词对词的翻译
他 向 记者 介绍了 主要 内容
He to reporters introduced main content

词序混乱，"He introduced main content to reporters"的概率显然更高。

什么是N元模型

N元模型是统计语言模型中最简单的一种。

有限视野假设 我们假设一个词和前面k个词相关 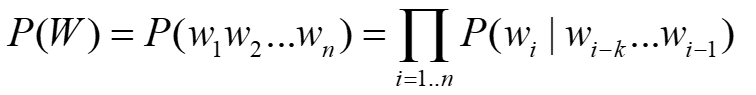上式我们称之为k阶马尔可夫链
e.g.
1阶马尔可夫链 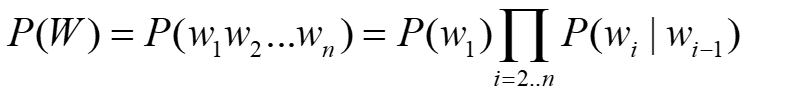2阶马尔可夫链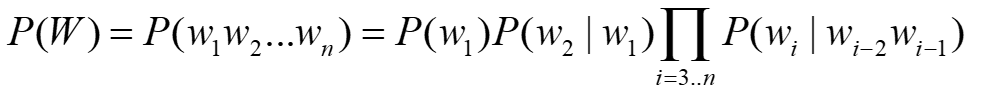

我们将N-1阶马尔科夫链称为N元语言模型。（N-Gram Language Model）。
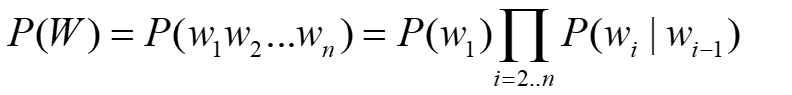2元模型
3元模型
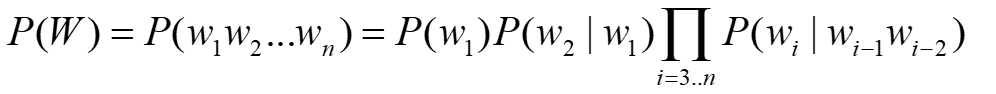其中的2元模型，也就是假设每个词和之前一个词有关。

n元模型中的参数

n元模型中的参数就是式子中的每个P，为了计算任意句子的P(w),我们必须获得任意单词之间的P(wi | wj wj+1 … wk)。其中wj wj+1 … wk的数量由n元模型中的n决定。

参数数量：

n越大，参数越多， 假设词汇量为20000
2元模型(1阶Markov)参数数量：20000^2
3元模型(2阶Markov)参数数量：20000^3
…
N元模型(N-1阶Markov)参数数量：20000^n

如何估计参数

对于已有语料。我们可以通过统计语料中的单词组合频率来获得这些参数。例如对于2元模型：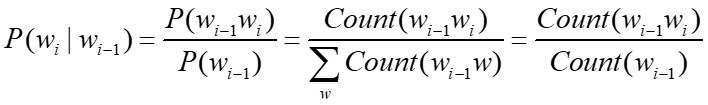
获得频率后，通过最大似然估计来估算参数，也就是概率P(wi | wj wj+1 … wk)。

参数如果为0？

参数P如果=0，零概率还会向下传播，一个2元或者3元文法的零概率，会导致整个句子的零概率。

参数为0经常出现吗

Zipf法则表明了参数为0是很常见的。
Zipf Law: 如果以词频排序，词频和排位的乘积是一个常数。
Zipf法则隐含的意义：大部分的词都稀有,语言中频繁出现的事件是有限的，不可能搜集到足够的数据来得到稀有事件的完整概率分布。词（一元）如此，对于二元、三元模型更加严重。

数据稀疏问题永远存在，因此我们需要处理参数为0的情况，处理方法有： – 构造等价类 – 参数平滑

参数平滑方法

平滑是指给没观察到的N元组合赋予一个概率值，以保证词序列总能通过语言模型得到一个概率值。

• 思想
  稍微减少已观察到的事件概率的大小，同时把少量概率分配到没有看到过的事件上，折扣法，使整个事件空间的概率分布曲线更加平滑。改进模型的整体效果。高概率调低点，小概率或者零概率调高点。
• 约束
  确保 ∑X∈Ω P(X)=1

几种常见方法：

Add counts

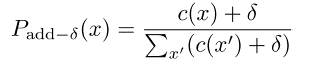效果不佳，一般并不使用。但是在文本分类中被使用。

Laplace smoothing/Dirichlet Prior

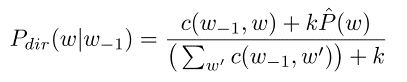
简单线性插值平滑

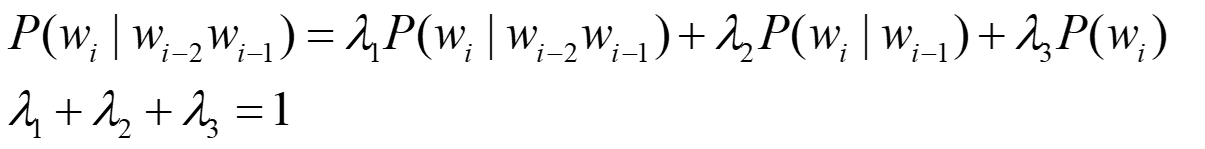线性插值平滑算法，也称为Jelinek-Mercer smoothing，其基本思想是将高阶模型和低阶模型作线性组合，利用低元N-gram模型对高元N-gram模型进行线性插值。因为在没有足够的数据对高元n-gram模型进行概率估计时，低元n-gram模型通常可以提供有用的信息。例如对于trigram：
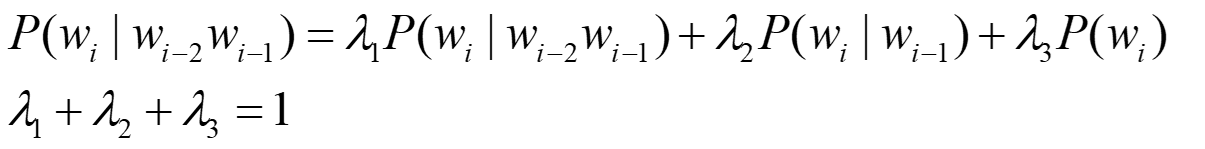其中的lambda可以通过在验证集上使用EM算法（最大期望）最大化困惑度得到。

验证集(Held-Out)
在获得语言模型时，对最初数据划分为Training Data，Held-Out Data，Test Data。其中验证集用于调整超参数。

Kneser-Ney Smoothing

最常用的平滑方法。 暂时略。

除了以上插值算法，此外还有Katz Smoothing等，作为细节内容，本文省略。

统计语言模型的评价

统计语言模型的评价的最佳方式显然是直接将模型应用于当前需要的应用,然后看看应用是否有所改进。这种端到端的评价我们称为外在评价（extrinsic evaluation），但是端到端的评价方式代价一般很大。因此我们需要一些内在评价（intrinsic evaluation）指标。

譬如对于N元模型，我们通过训练集数据获得模型，在测试集上评估模型好坏。可以计算测试集的概率，概率越大，我们认为模型越好。

困惑度

在实践中，我们不直接使用原始概率作为指标，而是困惑度（Perplexity）,也被简写为 PP。困惑度其实就是我们对语言模型评价的一个内在评价（intrinsic evaluation）指标。

对于一个测试集w1w2…wn，困惑度的定义如下，其实就是将句子概率的倒数，并开N次方。 其中4.15定义了一个统计语言模型的困惑度。4.16则是一个2元模型的困惑度。所以说，困惑度越小，概率越大，模型越好。

困惑度的物理含义

困惑度有很好的物理含义，它是在给定上下文条件下，句子中每个位置平均可以选择的单词数量。（《数学之美 第2版》P69）。一个模型困惑度越低，每个位置的词就越确定,模型越好。

困惑度越低，模型越好

Training 38 million words, test 1.5 million words, WSJ

N-gram Order	Unigram	Bigram	Trigram
Perplexity	962	170	109

值得注意的是，测试集中的词汇知识如果事先预支，并训练出模型，那么困惑度会人为降低，此时就不一定具有可比性了，因此如果要对比两个模型的好坏，要求他们使用相同的词汇。

熵

熵是信息的度量。 对于一个随机变量X，其熵H(X)如下式：

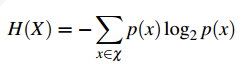
原则上，log的底可以任取，但是使用log2，那么熵的单位就是bit。
对熵的一种直观看法是：熵表明了用来编码信息的最小的比特数量。
信息论专注《Cover and Thomas》的一个例子：马赛比赛中有8匹马。由于Yonkers赛马场太远，我们无法去现场，因此我们传递比特信息给赌场告诉他那匹马会赢。为了表示8匹马，我们需要对其编码，第一匹马001，第二匹马010，依此类推。这样我们每场比赛都需要发送3bit信息。平均每场也是需要发送3bit信息。但是如果不同马的胜率概率分布不同，那么我们就有可能做到更优。譬如使用哈夫曼树就可以做到。

假设8匹马的胜率概率分布如下：

Horese id	p
1	1/2
2	1/4
3	1/8
4	1/16
5	1/64
6	1/64
7	1/64
8	1/64

马的胜率的随机变量X，我们对其计算熵，会得到一个更低的比特数。

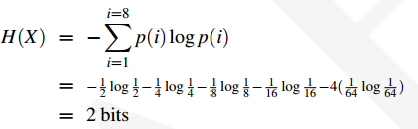
如果我们应用哈夫曼编码，对更可能赢的马使用更短的编码，其中1号马为0，其余的分别为110，1110，11110，111101，111110，1111101。那么平均每场比赛只需要2bit的数据。如果马的胜率都是均等的话，我们再计算信息熵：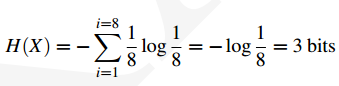

困惑度与熵的关系

结论

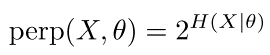
具体解释详见《参考读物-N元语言模型.pdf》4.6节 P20，本文概述如下：

熵的定义中，我们只是对单变量计算熵。但是如果我们要对n元模型中的语句计算信息熵，语句是由多个单词组成，每个单词都有其概率分布，如何计算整个句子的熵呢？我们首先将一个定长的单词序列作为一个变量，该变量的范围是定长句子中所有单词可能的组合。该变量的熵就是：

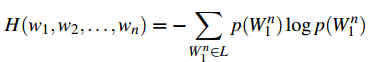
我们定义一个熵速率的概念，并将他当作是每个单词的熵值：

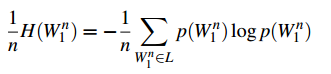
由于我们要对整个语言进行建模，因此我们让n趋向于无穷大，求其极限。

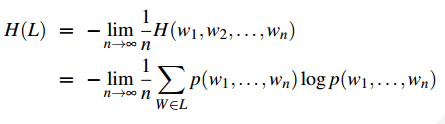
根据Shannon-McMillan-Breiman定理，如果一个语言在某种意义下是正则的（准确的说，如果预言既是平稳的，又是遍历的)

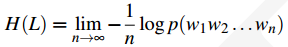
上式表明，我们可以通过一个足够长的单词序列来代表整个语言L，而非对语言中的所有可能的词序列都进行计算。Shannon-McMillan-Breiman定理的直觉出发点是，一个足够长的单词序列会包含很多短的单词序列，而这些短的单词序列根据他们的概率分布出现在长序列中。

交叉熵

当我们要计算产生数据的真实概率分布p，但是我们并不知道p，如果此时我们知道p的一个近似模型m，那么m在p上的交叉熵定义为：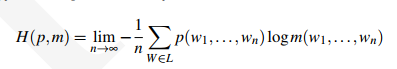
再次使用Shannon-McMillan-Breiman定理，我们会得到

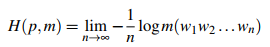
交叉熵有用的一个原因在于交叉熵是真实概率分布p的熵的上界。H(p,m)>=H(p)。因此可以通过使用一个近似模型,并用近似模型逼近真实模型。
前面的公式中我们用交叉熵近似了真实熵，其中交叉熵是对无线长度的单词序列进行计算的。在我们的n元模型中，我们把N取固定值，交叉熵为：

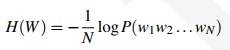
这时我们对上式的交叉熵计算2的交叉熵次方。发现恰好等于n元模型的复杂度。
所以我们说熵与困惑度的关系，其实讲的是交叉熵与困惑度的关系。

n元模型的实验

n越大模型越好。但是在语音识别中n>3代价很大。该图貌似还可以看出，线性平滑比katz好。

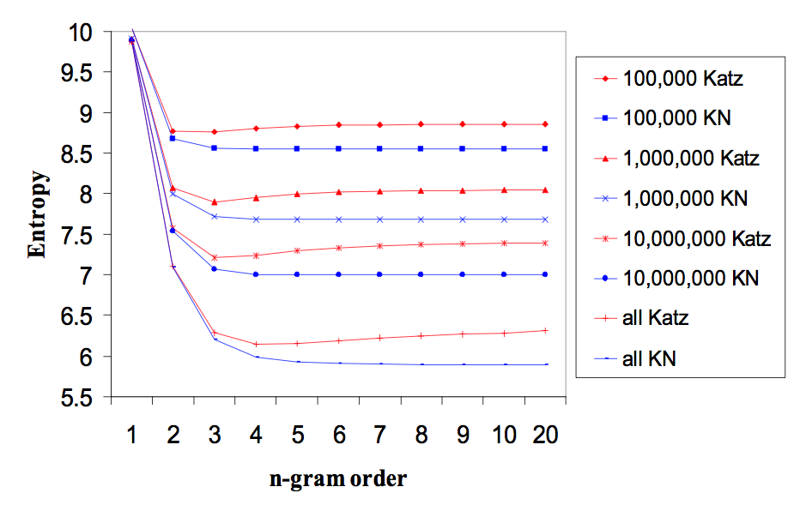
N元模型的评价

• 在很多方面取得了成功（Chelba 1998 Charniak 2001）
  • Speech Recognition
  • OCR
  • Context-sensitive spelling correction
• 从语言具有的特性看，显得过于简单和幼稚
  • Lexical
  • No long distance dependencies
  • No structure or syntactic dependency
• 一点个人评价
  N元模型是用统计方法对语言有限语料的建模方式，n-gram中的n越大，模型越好。因此越好的模型，在生成语句的任务中越不具有创造能力。
  考虑这样一个任务，英文单词由字母序列组成，我们对单词应用N元模型进行建模，这里的gram指的是字母。由于单词是有限的，我们可以通过词典直接训练单词模型。另一方面由于单词的字母序列长度有限，一般不超过30位，如果我们训练30元模型，得出的模型将是一个完备的单词模型。如果我们希望通过该模型生成新的词汇，我们的模型总是会推荐已有的词汇，对于未存在的词汇判定的概率则总是很低。

其他语言模型

其他计算P(w)的方法： – cache：以一个单词窗口作为条件 – grammer：以语法解析树作为条件

神经网络的方法：
省略，计划其他文档中详细学习。

参考文献

[1]南京大学计算机科学与技术系《自然语言处理》课程ppt,戴新宇,《统计自然语言处理》《统计语言模型》
[2]斯坦福CS 124课程材料《Language Modeling—Introduction to N-grams》
[3]Speech and Language Processing. Daniel Jurafsky & James H. Martin.Chapter4.N-Grams
[4]数学之美第2版（其中P68页作者声称相对熵在有些文献中被称为交叉熵，个人感觉有误，cross-entropy是另一个概念）